Predictive Analytics: Linear Models

Predictive models are used to predict outcomes of interest based on some known information. In order to come up with a good prediction rule, we can use historical data where the outcome is observed. This will allow us to calibrate the predictive model, i.e., to learn how specifically to link the known information to the outcome. For example, we might be interested in predicting the satisfaction of a user based on the user’s experience and interaction with a service: \[ S = f(X_1,X_2,X_3), \] where $S$ is the satisfaction measure and $X_1,X_2,X_3$ are three measures of experience. For example, $S$ could be satisfaction of a visitor to a theme park, $X_1$ could be an indicator of whether the visit was on a weekend or not, $X_2$ could be indicator of whether the visitor was visiting with kids or not and we could let $X_3$ could capture all other factors that might drive satisfaction. Then we could use a predictive model of the form \[ S = \beta_{wk} Weekend + \beta_f Family + X_3, \] where $Weekend=1$ for weekend visitors (otherwise zero), $Family=1$ for familily visitors (otherwise zero) and $\beta_{wk},\beta_f$ define the prediction rule. $X_3$ captures all other factors impacting satisfaction. We might not have a good idea about they are but we can let $\beta_0$ denote the mean of them. Then we can write the model as \[ S = \beta_0 + \beta_{wk} Weekend + \beta_f Family + \epsilon, \] where $\epsilon = X_3-\beta_0$ must have mean zero. This is a predictive model since it can predict mean satisfaction given some known information. For example, predicted satisfaction for non-family weekend visitors is $\beta_0 + \beta_{wk}$, while predicted mean satisfaction for family weekend visitors is $\beta_0 + \beta_{wk} + \beta_f$. Of course, these prediction rules are not all that useful if we don’t know what the $\beta$’s are. We will use historical data to calibrate the values of the $\beta$’s so that they give us good prediction rules.

The predictive model above is simple. However, we can add other factors to it, i.e., add things that might be part of $X_3$. For example, we might suspect that the total number of visitors in the park would influence the visit experience. We could add that to the model as a continuous measure: \[ S = \beta_0 + \beta_{wk} Weekend + \beta_f Family + \beta_n N + \epsilon, \] where $N$ is the number of visitors on the day that $S$ was recorded (for example on a survey). We can now make richer predictions. For example, what is the satisfaction of a family visitor on a non-weekend where the total park attendance is $N=5,000$?

Predictive models like these are referred to as “linear”, but that’s a bit of a misnomer. The model above implies that satisfaction is a linear function of attendance $N$. However, we can change that by specifying an alternative model. Suppose we divide attendance into three categories, small, medium and large. Then we can use a model of the form: \[ S = \beta_0 + \beta_{wk} Weekend + \beta_f Family + \beta_{med} D_{Nmed} + \beta_{large} D_{Nlarge} + \epsilon, \] where $D_{Nmed}$ is an indicator for medium sized attendance days (equal to 1 on such days and zero otherwise) and $D_{Nlarge}$ the same for large attendance days. Now the relationship between attendance size and satisfaction is no longer restricted to be linear. If desired you can easily add more categories of attendance to get finer resolution.

Exercise

Using the last model above, what would the predicted mean satisfaction be for family visitors on small weekend days? How about on large weekend days?

In the following we will consider two case studies. All data and code are in the project in this zip file.

Case Study: Pricing a Tractor

WWW Let’s use predictive analytics to develop a “blue book” for tractors: Given a set of tractor characteristics, what would we expect the market’s valuation to be?

The dataset auction_tractor.rds contains information on 12,815 auction sales of a specific model of tractor. These auctions occurred in many states across the US in the years 1989-2012. We will develop a model to predict auction prices for tractors given the characteristics of the tractor and the context of the auction. The data has been split into a test and training sample. The objective is to predict the prices in the test sample.

Let’s start by loading the training data and finding out what information is in it:

## get libraries 
library(tidyverse)
library(forcats)

## read data, calculate age of each tractor and create factors 
train <- read_rds('data/auction_tractor_train.rds') %>%
  mutate(MachineAge = saleyear - YearMade,  
         saleyear=factor(saleyear),
         salemonth=factor(salemonth,levels=month.abb),
         saleyearmonth = paste(saleyear,salemonth))

names(train)

##  [1] "SalesID"                  "SalePrice"               
##  [3] "MachineID"                "ModelID"                 
##  [5] "datasource"               "auctioneerID"            
##  [7] "YearMade"                 "MachineHoursCurrentMeter"
##  [9] "UsageBand"                "saledate"                
## [11] "fiModelDesc"              "fiBaseModel"             
## [13] "fiSecondaryDesc"          "fiModelSeries"           
## [15] "fiModelDescriptor"        "ProductSize"             
## [17] "fiProductClassDesc"       "state"                   
## [19] "ProductGroup"             "ProductGroupDesc"        
## [21] "Drive_System"             "Enclosure"               
## [23] "Forks"                    "Pad_Type"                
## [25] "Ride_Control"             "Stick"                   
## [27] "Transmission"             "Turbocharged"            
## [29] "Blade_Extension"          "Blade_Width"             
## [31] "Enclosure_Type"           "Engine_Horsepower"       
## [33] "Hydraulics"               "Pushblock"               
## [35] "Ripper"                   "Scarifier"               
## [37] "Tip_Control"              "Tire_Size"               
## [39] "Coupler"                  "Coupler_System"          
## [41] "Grouser_Tracks"           "Hydraulics_Flow"         
## [43] "Track_Type"               "Undercarriage_Pad_Width" 
## [45] "Stick_Length"             "Thumb"                   
## [47] "Pattern_Changer"          "Grouser_Type"            
## [49] "Backhoe_Mounting"         "Blade_Type"              
## [51] "Travel_Controls"          "Differential_Type"       
## [53] "Steering_Controls"        "saleyear"                
## [55] "salemonth"                "MachineAge"              
## [57] "saleyearmonth"

The key variable is “SalePrice” - the price determined at auction for a given tractor. There is information about the time and location of the auction and a list of tractor characteristics.

Summarizing the data

Before you start fitting predictive models, it is usually a good idea to summarize the data to get a basic understanding of what is going on. Let’s start by plotting the observed distribution of prices:

## distribution of prices
train %>%
  ggplot(aes(x=SalePrice/1000)) + geom_histogram(binwidth=10)  + xlab("Sale Price (in $1,000)")

There is a quite a bit of variation in the observed prices with most prices being in the $25K to $75K range. Did prices change over the time period? Let’s check:

## average auction price by year of sale
train %>%
  group_by(saleyear) %>%
  summarize('Average Sale Price ($)' = mean(SalePrice),
            'Number of Sales' =n()) %>%
  gather(measure,value,-saleyear) %>%
  ggplot(aes(x=saleyear,y=value,group=measure,color=measure)) + 
  geom_point(size=3) + 
  geom_line(linetype='dotted') + 
  facet_wrap(~measure,scales='free')+
  xlab('Year of Sale')+ylab(' ')+
  theme(legend.position="none",
        axis.text.x = element_text(angle = 45, hjust = 1))

The average price increased by about $20K over the time period. Like cars, tractors depreciate with age. Let’s see how this is reflected in the price at auction:

train %>%
  filter(MachineAge >= 0) %>%
  mutate(MachineAgeCat = cut(MachineAge,
                    breaks=c(0,2,4,6,10,15,100),
                    include.lowest=T,
                    labels = c('<= 2','3-4','5-6','7-10','11-15','>15'))) %>%
  group_by(saleyear,MachineAgeCat) %>%
  summarize(mp = mean(SalePrice)/1000,
            'Number of Sales' =n()) %>%
  ggplot(aes(x=MachineAgeCat,y=mp,group=saleyear,color=factor(saleyear))) + 
  geom_point(size=2) + 
  geom_line() + 
  xlab('Machine Age in Years')+ylab('Average Sale Price (in $1000)')+
  facet_wrap(~saleyear,scales='free')+
  theme(legend.position="none",
        axis.text.x = element_text(angle = 45, hjust = 1,size=8))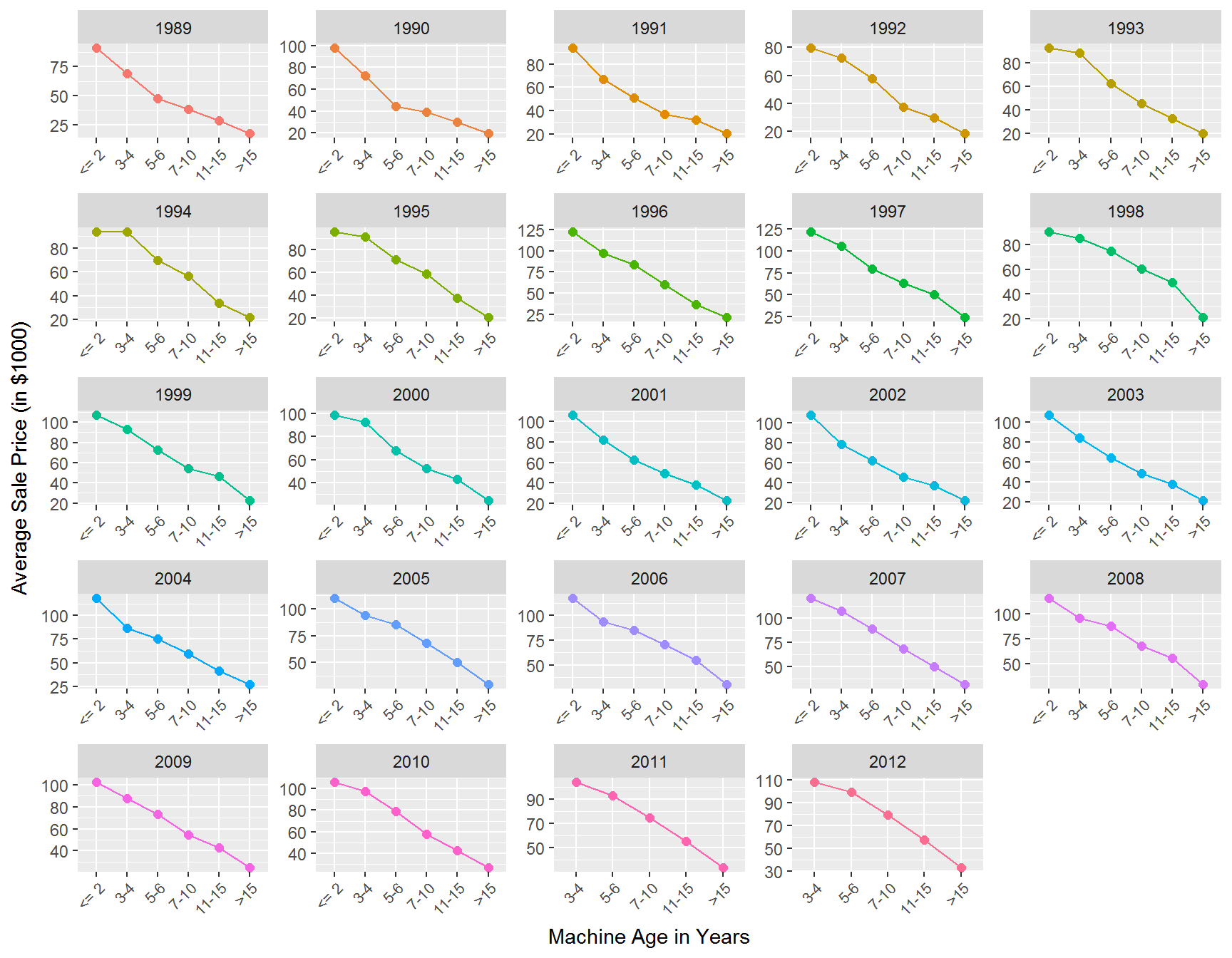

The tractor model in the data has been sold as different sub-models (or “trim”) over time. Let’s see how prices vary across sub-models:

train %>%
  group_by(saleyear,fiSecondaryDesc) %>%
  summarize(mp = mean(SalePrice)/1000,
            ns =n()) %>%
  ggplot(aes(x=saleyear,y=mp,group=fiSecondaryDesc,color=fiSecondaryDesc)) + 
  geom_point(size=2) + 
  geom_line() + 
  xlab('Year of Sale')+ylab('Average Sale Price (in $1,000)')+
  facet_wrap(~fiSecondaryDesc,scales='free')+
  theme(legend.position="none",
        axis.text.x = element_text(angle = 45, hjust = 1,size=7))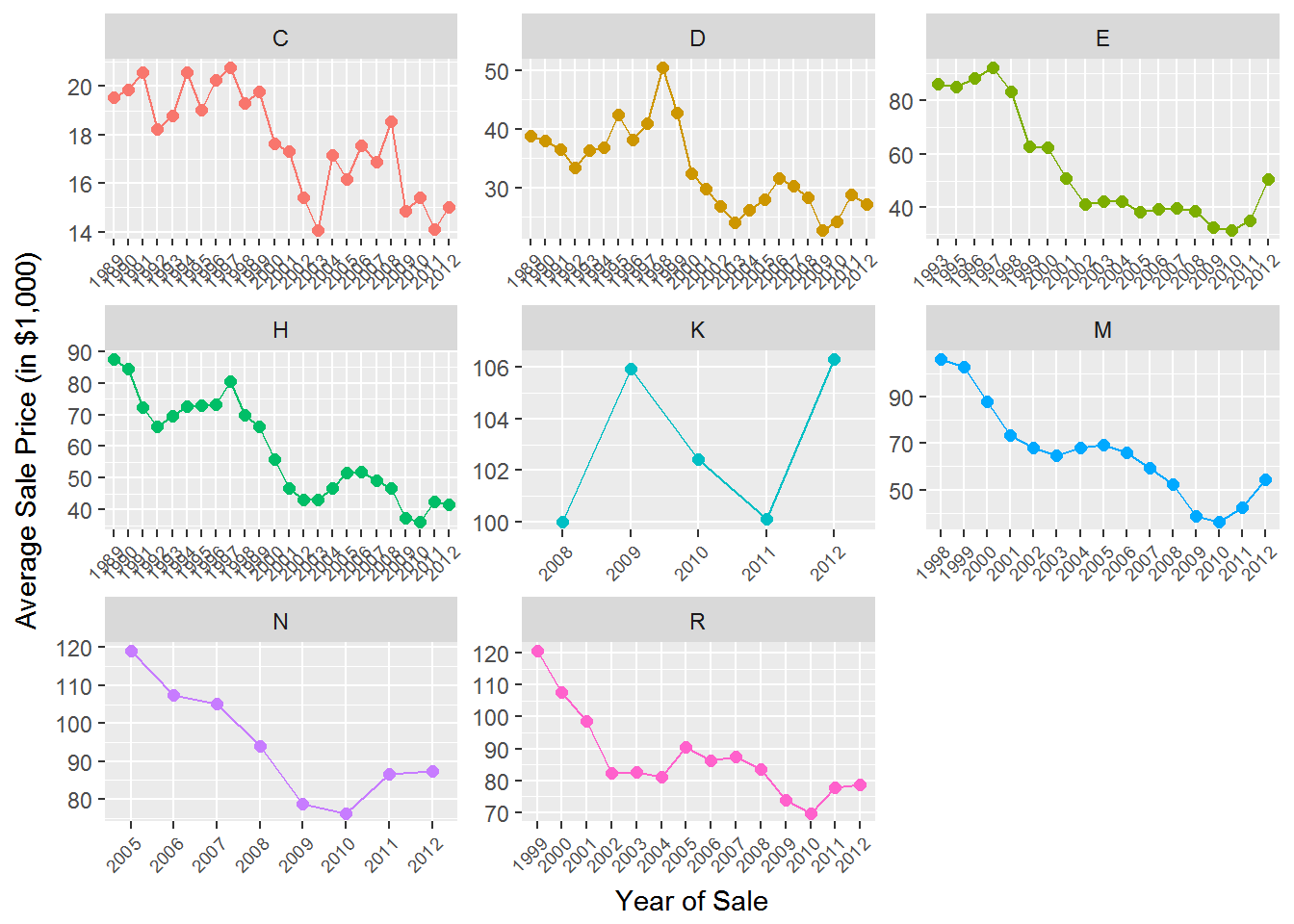

Finally, let’s see how prices vary across states:

train %>%
  group_by(state) %>%
  summarize(mean.price = mean(SalePrice)/1000) %>%
  ggplot(aes(x=fct_reorder(state,mean.price),y=mean.price)) + 
  geom_bar(stat='identity') + 
  ylab('Average Sale Price (in $1,000)')+
  theme(axis.text.x = element_text(angle = 90, hjust = 1))+
  xlab('State')

What to take away from these summaries? Well, clearly we can conclude that any predictive model that we might consider should at a minimum account for year, state, sub-model and machine age effects.

Predictive Models

We start by defining the data used for developing the model. Since we will want to have state effects in the model, let’s elminate states with too few sales:

incl.states <-  train %>%
  count(state) %>%
  filter(n > 10, !state=='Unspecified')

train <- train %>%
  filter(state %in% incl.states$state) 

test <- read_rds('data/auction_tractor_test.rds') %>%
  filter(state %in% incl.states$state) %>%
  mutate(MachineAge = saleyear - YearMade,  
         saleyear=factor(saleyear,levels=levels(train$saleyear)),
         salemonth=factor(salemonth,levels=month.abb),
         saleyearmonth = paste(saleyear,salemonth))

Let’s start with a model that is clearly too simple: A model that predicts prices using only the year of sale. We already know from the above plots that we can do better, but this is just to get started. You specify a linear model in R using the lm command:

## linear model using only year to predict prices
lm.year <- lm(log(SalePrice)~saleyear,
              data = train)

## look at model estimates 
sum.lm.year <- summary(lm.year)

This is a linear model where we are predicting the (natural) log of sale price using the factor saleyear. When predicting things like prices (or sales), it is usually better to predict the log of price (or sales). The object sum.lm.year contains the calibrated (or estimated) coefficients for your model (along with other information):

## 
## Call:
## lm(formula = log(SalePrice) ~ saleyear, data = train)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.89955 -0.39590  0.05271  0.46406  1.28644 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  10.35752    0.04242 244.194  < 2e-16 ***
## saleyear1990  0.12184    0.06196   1.967 0.049266 *  
## saleyear1991  0.17394    0.05877   2.960 0.003086 ** 
## saleyear1992 -0.02255    0.05649  -0.399 0.689713    
## saleyear1993  0.03718    0.05710   0.651 0.514984    
## saleyear1994  0.09766    0.05825   1.676 0.093692 .  
## saleyear1995  0.17757    0.05884   3.018 0.002550 ** 
## saleyear1996  0.20155    0.05897   3.418 0.000634 ***
## saleyear1997  0.29207    0.05771   5.061 4.25e-07 ***
## saleyear1998  0.37140    0.05293   7.017 2.41e-12 ***
## saleyear1999  0.44484    0.05478   8.121 5.16e-16 ***
## saleyear2000  0.33765    0.04876   6.924 4.65e-12 ***
## saleyear2001  0.25108    0.04908   5.115 3.19e-07 ***
## saleyear2002  0.26864    0.05136   5.230 1.73e-07 ***
## saleyear2003  0.16949    0.05177   3.274 0.001065 ** 
## saleyear2004  0.34191    0.04950   6.908 5.22e-12 ***
## saleyear2005  0.44718    0.05045   8.863  < 2e-16 ***
## saleyear2006  0.53522    0.05009  10.685  < 2e-16 ***
## saleyear2007  0.52924    0.04901  10.799  < 2e-16 ***
## saleyear2008  0.51686    0.04764  10.850  < 2e-16 ***
## saleyear2009  0.46650    0.04682   9.963  < 2e-16 ***
## saleyear2010  0.38935    0.04805   8.103 5.99e-16 ***
## saleyear2011  0.55977    0.04691  11.933  < 2e-16 ***
## saleyear2012  0.51798    0.05516   9.390  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5923 on 10122 degrees of freedom
## Multiple R-squared:  0.06978,    Adjusted R-squared:  0.06766 
## F-statistic: 33.01 on 23 and 10122 DF,  p-value: < 2.2e-16

Notice that while we have data from 1989 to 2012, there is no effect for 1989 - the model dropped this automatically. Think of the intercept as the base level for the dropped year - the average log price in 1989. The predicted average log price in 1990 is then 0.122 higher. Why? Like in the satisfaction example above, you should think of each effect as being multiplied by a one or a zero depending on if the year correspond to the effect in question (here 1990). This corresponds to an increase in price of about 12%. Similarly, the predicted average log price in 1991 would be 10.36+0.174.

In order to plot the estimated year effects it is convenient to put them in a R data frame. We can also attach measures of uncertainty of the estimates (confidence intervals) at the same time:

## put results in a data.frame using the broom package
library(broom)
results.df <- tidy(lm.year,conf.int = T)

We can now plot elements of this data frame to illustrate effects. We can use a simple function to extract which set of effects to plot. Here there is only saleyear to consider:

## ------------------------------------------------------
## Function to extract coefficients for plots 
## ------------------------------------------------------
extract.coef <- function(res.df,var){
  res.df %>%
    filter(grepl(var,term)) %>%
    separate(term,into=c('var','level'),sep=nchar(var))
}
##-------------------------------------------------------


## plot estimated trend
extract.coef(results.df,"saleyear") %>%
  ggplot(aes(x=level,y=estimate,group=1)) + 
  geom_point() + 
  geom_line(linetype='dotted')+
  geom_hline(aes(yintercept=0))+
  theme(axis.text.x = element_text(angle = 90, hjust = 1))

This plot closely resembles the plot above of average prices per year. This is not strange since our “model” basically just calculates the average log price per year.

If you want to add confidence intervals to the plot, you can use the geom_pointrange option:

extract.coef(results.df,"saleyear") %>%
  ggplot(aes(x=level,y=estimate,ymin=conf.low,ymax=conf.high,group=1)) + 
  geom_pointrange() + 
  geom_line(linetype='dotted')+
  geom_hline(aes(yintercept=0))+
  theme(axis.text.x = element_text(angle = 90, hjust = 1))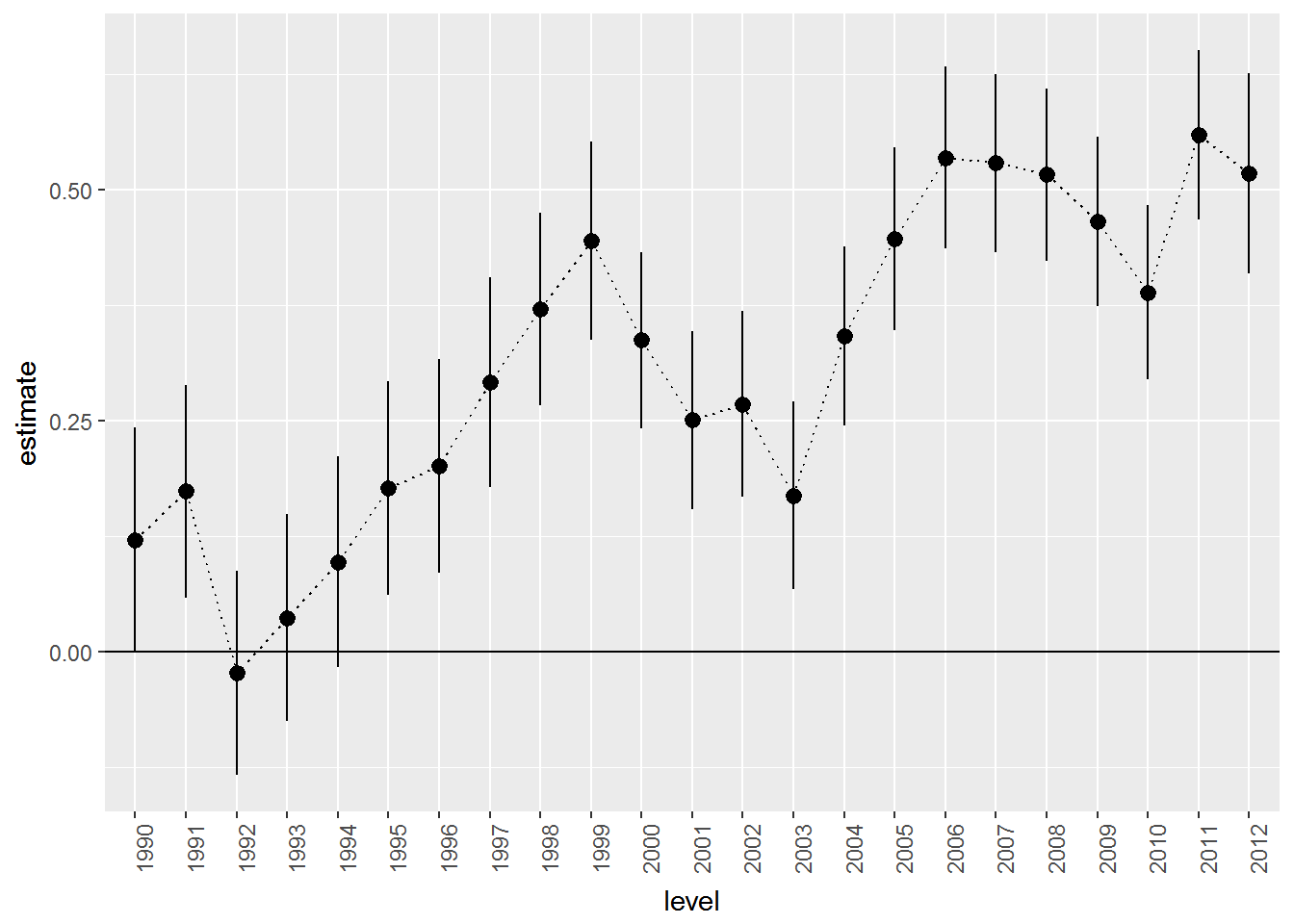

This model would be just fine if the main driver of variation in sale prices was a time trend. This is clearly false. One indication is to look at the with-in sample fit. For example, in the output above it says “Multiple R-squared: 0.06978”. This means that the annual time trend only explains 7% of the overall variation in log prices. That is not a good predictive model. We can also evaluate the fit to the test data. Let’s grab the test data and predict the prices using our model and then compare to what the prices actually were:

pred.df <- data.frame(log.sales = log(test$SalePrice),
                      log.sales.pred = predict(lm.year,newdata = test))

pred.df %>%  
  ggplot(aes(x=log.sales,y=log.sales.pred)) + geom_point(size=2)  + 
  xlab('Actual Log Prices') + ylab('Predicted Log Prices')

Yikes….not a good set of predictions: Actual log prices vary from 9 to over 11.5 and out predictions are kind of pathetic - only varying between 10.3 and 10.9.

Let’s consider a model that takes into account that auctions occur throughout the year and across many states. We do this by including month and state effects:

lm.base <- lm(log(SalePrice)~state + saleyear + salemonth,
              data = train)

results.df <- tidy(lm.base,conf.int = T)

We wont show the estimated coefficients here (since there are too many of them), but this model explains 12.2% of the overall variation in log prices in the estimation sample. That’s better than before but we have also included more effects. How about in terms of predictions? Let’s check:

pred.df <- data.frame(log.sales = log(test$SalePrice),
                      log.sales.pred = predict(lm.base,newdata=test))

pred.df %>%  
  ggplot(aes(x=log.sales,y=log.sales.pred)) + geom_point(size=2)  + geom_line(aes(x=log.sales,y=log.sales))+
  xlab('Actual Log Prices') + ylab('Predicted Log Prices') + coord_fixed()

Here we have added a 45 degree line to the plot. Our predictions are slightly better than before but still not great. Let’s add information about the sub-model of each tractor:

lm.trim <- lm(log(SalePrice)~state+saleyear+salemonth + fiSecondaryDesc,
              data = train)

results.trim.df <- tidy(lm.trim,conf.int = T)

With this model we are explaining 79.4% of the overall variation in log prices. Let’s plot the predictions with information about each model type:

pred.df <- data.frame(log.sales = log(test$SalePrice),
                      log.sales.pred = predict(lm.trim,newdata=test),
                      trim = test$fiSecondaryDesc)

pred.df %>%  
  ggplot(aes(x=log.sales,y=log.sales.pred)) + geom_text(aes(color=trim,label=trim),size=2) + 
  geom_line(aes(x=log.sales,y=log.sales)) + 
  xlab('Actual Log Prices') + ylab('Predicted Log Prices') + coord_fixed() + 
  theme(legend.position="none")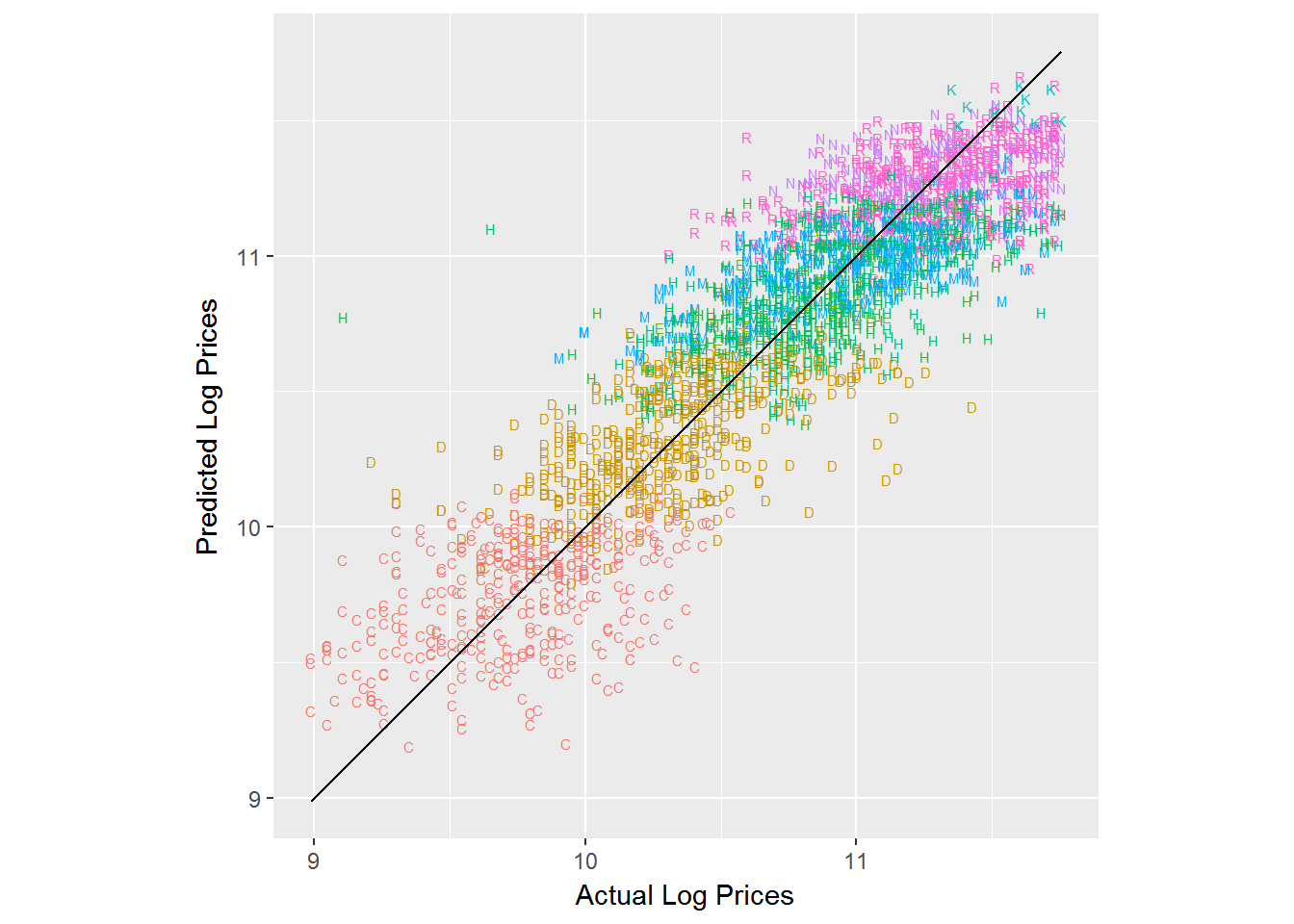

Ok - we are getting close to something useful. But we saw from the plots above that the age of the tractor was important in explaining prices so let’s add that to the model as a factor:

train <- train %>%
  filter(MachineAge >= 0) %>%
  mutate(MachineAgeCat = cut(MachineAge,
                             breaks=c(0,2,4,6,10,15,100),
                             include.lowest=T,
                             labels = c('<= 2','3-4','5-6','7-10','11-15','>15')))

lm.trim.age <- lm(log(SalePrice)~state+saleyear+salemonth + fiSecondaryDesc+MachineAgeCat,
                  data = train)

results.trim.age.df <- tidy(lm.trim.age,conf.int = T)

Now we are explaining 85.7% of the overall variation in log prices. Let’s take a closer look at the estimated age effects:

extract.coef(results.trim.age.df,"MachineAgeCat") %>%
  mutate(level = factor(level,levels=levels(train$MachineAgeCat))) %>%
  ggplot(aes(x=level,y=estimate,ymin=conf.low,ymax=conf.high,group=1)) +
  geom_pointrange() + geom_line(linetype='dotted')+
  geom_hline(aes(yintercept=0))+
  theme(axis.text.x = element_text(angle = 90, hjust = 1))+
  xlab('Machine Age')

We can think of this as an age-depreciation curve. Compared to two year old (or less) tractors, 3 to 4 year old tractors are on average word 0.196 less on the log-price scale. This corresponds to exp(0.196)-1 = 21.7% percent. 11 to 15 year old tractors are worth exp(0.768)-1=115% less than two year old or younger tractors.

We can also look at where tractors are cheapest by looking at the state effects:

extract.coef(results.trim.age.df,"state") %>%
  ggplot(aes(x=reorder(level,estimate),y=estimate,ymin=conf.low,ymax=conf.high,group=1)) + 
  geom_pointrange() + 
  geom_hline(aes(yintercept=0))+
  theme(axis.text.x = element_text(angle = 90, hjust = 1))+
  xlab('State')

Tractors are cheapest in Idaho, Michagan and New York and most expensive in Oklahoma, Nevada and North Dakota.

Finally, here are the predictions for the predictive model with age included:

test <- test %>%
  filter(MachineAge >= 0) %>%
  mutate(MachineAgeCat = cut(MachineAge,
                             breaks=c(0,2,4,6,10,15,100),
                             include.lowest=T,
                             labels = c('<= 2','3-4','5-6','7-10','11-15','>15')))


pred.df <- data.frame(log.sales = log(test$SalePrice),
                      log.sales.pred = predict(lm.trim.age,newdata = test),
                      trim = test$fiSecondaryDesc)

pred.df %>%  
  ggplot(aes(x=log.sales,y=log.sales.pred)) + geom_text(aes(color=trim,label=trim),size=2) + 
  geom_line(aes(x=log.sales,y=log.sales)) + 
  xlab('Actual Log Prices') + ylab('Predicted Log Prices') + coord_fixed() + 
  theme(legend.position="none")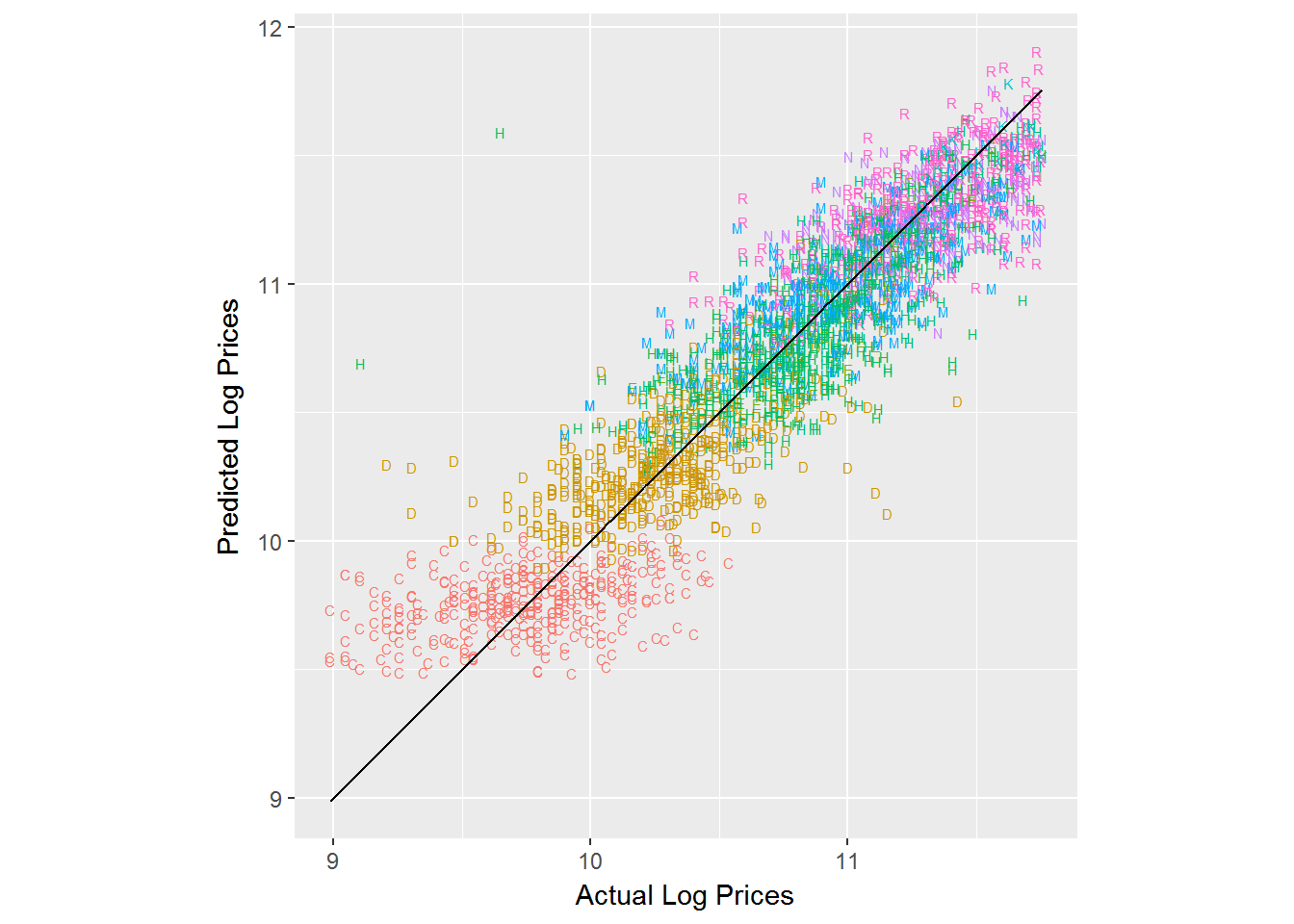

It is often useful to calculate summary measures of the predictions of the different models. Here we calculate two metrics: Mean Absolute Prediction Error and Root Mean Square Prediction Error. The smaller these are, the better is the predictive ability of the model. Both of these metrics are on the same scale as the outcome variable, log price.

pred.df <- data.frame(log.sales = log(test$SalePrice),
                      Year = predict(lm.year,newdata = test),
                      Base = predict(lm.base,newdata = test),
                      Trim = predict(lm.trim,newdata = test),
                      Time_Age = predict(lm.trim.age,newdata = test))

pred.df %>%
  gather(model,pred,-log.sales) %>%
  group_by(model) %>%
  summarize(MAE = mean(abs(log.sales-pred)),
            RMSE = sqrt(mean((log.sales-pred)**2))) %>%
  gather(metric,value,-model) %>%
  ggplot(aes(x=model,y=value,fill=model)) + geom_bar(stat='identity') + facet_wrap(~metric)+theme(legend.position="none")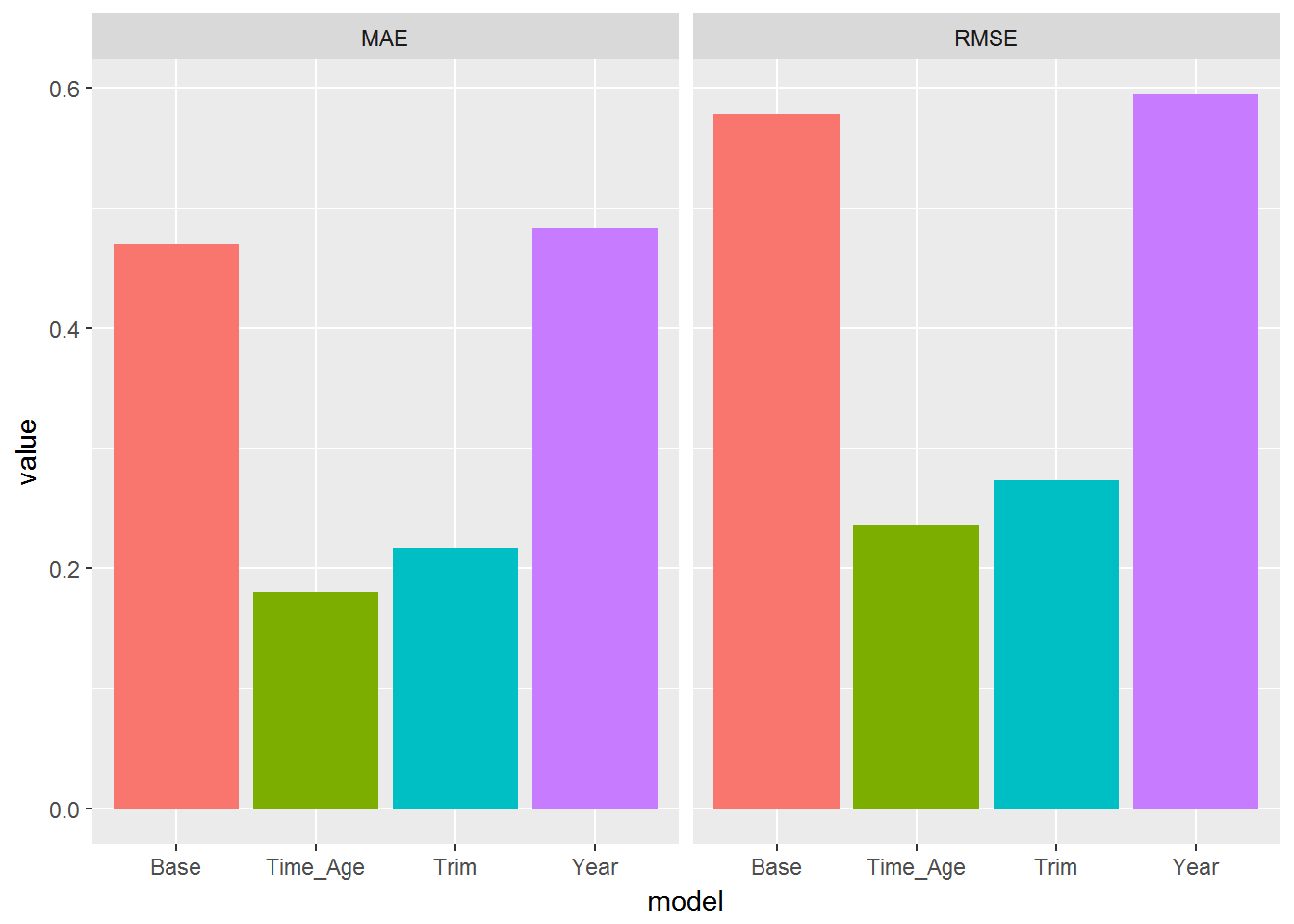

For both metrics we see that the model with both trim and age seems to do the best. It also had the best in-sample performance. Using this model we have an average absolute prediction error of a little less than .2 on the log scale. Depending on the type of use of this predictive model this may and may not be an acceptable error.

Exercise

We still haven’t used any of the specific tractor characteristics as additional predictive information. Try to add Enclosure (the type of “cabin” of the tractor), Travel_Controls (part of controlling the machine) and Ripper (the attachment that goes in the ground top cultivate the soil). You need to throw out data since there is limited information for some of the levels of these variables. You can verify this as follows:

table(train$Enclosure)

## 
##      EROPS   EROPS AC EROPS w AC      OROPS 
##        874          1       2904       6367

table(train$Travel_Controls)

## 
##  Differential Steer          Finger Tip               Lever 
##                2590                 811                  61 
## None or Unspecified               Pedal 
##                6675                   3

table(train$Ripper)

## 
##         Multi Shank None or Unspecified        Single Shank 
##                1073                8289                 778 
##                 Yes 
##                   1

You should drop the data for those levels with only very few auctions:

train <- train %>%
  filter(!Ripper=='Yes',!Travel_Controls=='Pedal',!Enclosure=='EROPS AC')

test <- test %>%
  filter(!Ripper=='Yes',!Travel_Controls=='Pedal',!Enclosure=='EROPS AC')

Case Study: Weather Patterns and Bike Commuting

WWW Let’s see how weather impacts bike demand in New York City’s citibike system. The data file bike_demand.rds contains trip data for three months, June-August 2015, aggregated to the hourly level. Each row in the data is a month-day-hour record with the total number of trips occurring in that month-day-hour window. The data file also contains day-hour weather information for the smae three month period. These have been scraped of the web from the web-site www.wunderground.com.

The weather data was merged with the bike trip data at the month-day-hour level. We can now investigate how sensitive bike demand is to weather. Here we will analyze the aggregate demand data. In an exercise you can try to see whether the results on the aggregate data is replicated on the two individual user segments present in the data. It is also possible to carry out the analysis by segmenting demand spatially, e.g., demand at individual bike stations.

We start by loading the data and then setting up a model that has weekday and hour effects along with rain, temperature and humidity effects:

bike.demand <- read_rds('data/bike_demand.rds')

lm.bike <- lm(log(n)~weekday+hour+RainCat+TempCat+HumidCat,data=bike.demand)

bike.results <- tidy(lm.bike,conf.int=T)

First, let’s look at effects of rain on bike demand:

extract.coef(bike.results,"RainCat") %>%
  ggplot(aes(x=level,y=estimate,ymin=conf.low,ymax=conf.high,group=1)) +
  geom_pointrange() + geom_line(linetype='dotted')+
  geom_hline(aes(yintercept=0))+
  theme(axis.text.x = element_text(angle = 45, hjust = 1))+
  xlab('Amount of Rain (Inches)')+
  ggtitle('Rain Effects on Bike Demand')

The left level is 0.00, i.e., no precipitation. These are large effects. A small amount of rain, less than 0.05 inches, reduces demand by .58 on the log scale. This is equivalent to a exp(-0.58)-1=44% drop in number of trips! The effects are even more dramatic for large amounts of rain. Note that the effect is slightly smaller for the largest rain level compared to the medium sized levels. Why might that be?

Here are the effects of temperature:

extract.coef(bike.results,"TempCat") %>%
  ggplot(aes(x=level,y=estimate,ymin=conf.low,ymax=conf.high,group=1)) +
  geom_pointrange() + geom_line(linetype='dotted')+
  geom_hline(aes(yintercept=0))+
  theme(axis.text.x = element_text(angle = 90, hjust = 1))+
  xlab('Temperature (F)')+
  ggtitle('Temperature Effects on Bike Demand')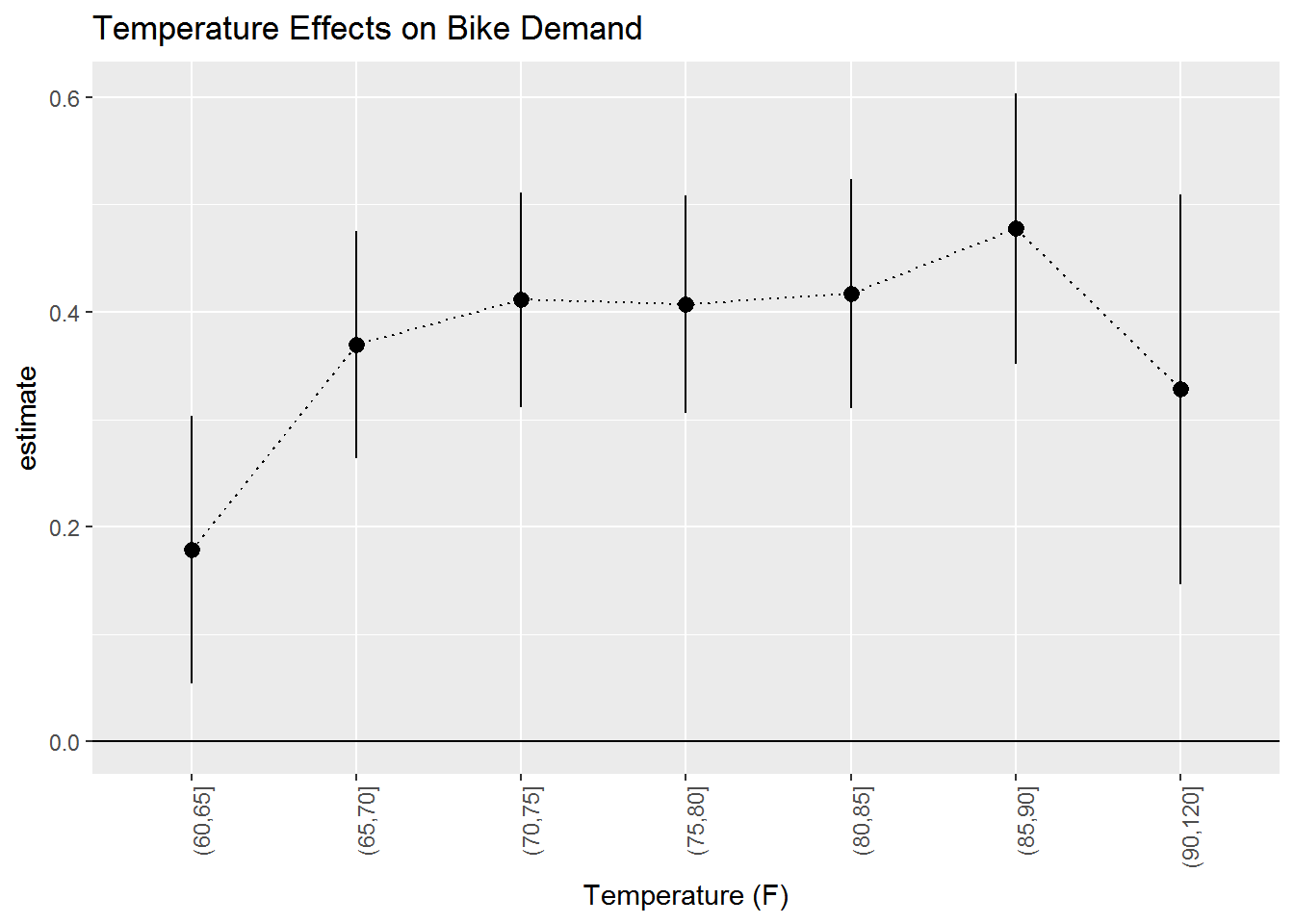

This is an inverse U-shape: Compared to the coolest days, trip demand increases with warmer temperatures and then levels off. For the hottest days we see a slight decline in trip demand (although this is not very precisely estimated).

Here are the effects of humidity:

extract.coef(bike.results,"HumidCat") %>%
  ggplot(aes(x=level,y=estimate,ymin=conf.low,ymax=conf.high,group=1)) +
  geom_pointrange() + geom_line(linetype='dotted')+
  geom_hline(aes(yintercept=0))+
  theme(axis.text.x = element_text(angle = 90, hjust = 1))+
  xlab('Percent Humidity')+
  ggtitle('Humidity Effects on Bike Demand')

Increasing humidity reduces demand for bikes. Very high humidity strongly reduces demand.

Exercise

The data file bike_demand_usertype.rds is structured the same way as the file above, except there are twice as many rows - one month-day-hour record for each user type (“Customer” and “Subscriber”). Redo the analysis above for each segment - do you find the same effects?

Regularizing a Predictive Model: Feature Selection using LASSO

When working with predicitive models, you will often be in the following situation: You have a potentially very large list of predictor variables to use and little theory for which to include in the model. How do you proceed? It is tempting to just use all of them. However, as the list of predictor variables grow, you will typically start to lose precision in your effects (i.e., the confidence intervals gets wider) and - as a result - your fit in the test sample make get much worse. But this then raises another problem: Which should be dropped from the model? This is the problem of variable or feature selection. There are a number of different frameworks to use - here we will focus on LASSO.

LASSO is short for Least Absolute Shrinkage and Selection Operator (say that ten times!). It is a useful tool for selecting relevant predictor variables in situations where the number of predictors is large (relative to the number of observations). The standard method for calibrating a linear model on the training data is Ordinary Least Squares. This method finds the coefficients that minimizes the sum of squared errors in the training sample. This method has intuitive appeal and can be shown to have certain desirable properties. However, it can get into trouble when the number of predictors - or “features” - gets large. In this case it is useful to “regularize” your model. What this means requires a little math. Ordinary Least Squares picks the list of coefficients $\beta$ by minimizing the sum of least squares:

\[ \sum_{i=1}^N (y_i - \sum_{k=1}^K x_{ik}\beta_k)^2. \] Regularization works by adding an extra term in this objective function. LASSO works by using minimizing \[ \sum_{i=1}^N (y_i - \sum_{k=1}^K x_{ik}\beta_k)^2 + \lambda \sum_{k=1}^K |\beta_k| \] The added term in the objective function acts to penalize large $\beta$ coefficients. $\lambda$ is a parameter that controls the degree of penalization. One can show that if a certain predictor, e.g., $x_{k}$, increase the sum of squares, then the second term will act to force the associated coefficient to zero. Therefore, LASSO is a tool for selecting a small number of relevant predictors out of a large list. The resulting model will often have superior predictive ability compared to the non-penalized version. Let’s demonstrate this using the tractor price case study. Note: We are skipping over some of the more technical aspects of LASSO. For example, there is also a regression variance parameter $\sigma$ in the objective function above. See here for more detail.

Case Study: Pricing a Tractor with LASSO

Suppose we want to predict tractor auction prices for states in the South Eastern region of the US. We start by importing the data and make a few transformations similar to the example above:

library(tidyverse)
library(glmnet)     # package with LASSO functions

statesIncl <- c("Louisiana","Arkansa","Tennessee","North Carolina","Mississippi",
                "Maryland","Georgia","South Carolina","Alabama")

train <- readRDS('data/auction_tractor_train.rds') %>%
  filter(state %in% statesIncl) %>%
  mutate(MachineAge = saleyear - YearMade,  
         saleyear=factor(saleyear),
         salemonth=factor(salemonth,levels=month.abb),
         saleyearmonth = paste(saleyear,salemonth)) %>%
  filter(MachineAge >= 0) %>%
  mutate(MachineAgeCat = cut(MachineAge,
                             breaks=c(0,2,4,6,10,15,100),
                             include.lowest=T,
                             labels = c('<= 2','3-4','5-6','7-10','11-15','>15'))) %>%
  filter(!Ripper=='Yes',!Travel_Controls=='Pedal',!Enclosure=='EROPS AC') 

test <- readRDS('data/auction_tractor_test.rds') %>%
  filter(state %in% statesIncl) %>%
  mutate(MachineAge = saleyear - YearMade,  
         saleyear=factor(saleyear,levels=levels(train$saleyear)),
         salemonth=factor(salemonth,levels=month.abb),
         saleyearmonth = paste(saleyear,salemonth)) %>%
  filter(MachineAge >= 0) %>%
  mutate(MachineAgeCat = cut(MachineAge,
                             breaks=c(0,2,4,6,10,15,100),
                             include.lowest=T,
                             labels = c('<= 2','3-4','5-6','7-10','11-15','>15'))) %>%
  filter(!Ripper=='Yes',!Travel_Controls=='Pedal',!Enclosure=='EROPS AC')

The functions in the glmnet package requires that you pass the data as one array of predictor variabels and another array with the dependent variable. This is easy enough to do by using the model.matrix function. Here we will try to fit a model with many predictor variables:

xTrain <- model.matrix(~state + saleyear + salemonth + fiSecondaryDesc + MachineAgeCat + Ripper + 
                       Travel_Controls + Enclosure + 
                       Transmission + Blade_Type + 
                       fiSecondaryDesc*MachineAgeCat + 
                       Enclosure*MachineAgeCat + 
                       Ripper*MachineAgeCat + 
                       Blade_Type*MachineAgeCat +
                       state*saleyear + 
                       state*MachineAgeCat + 
                       state*fiSecondaryDesc +
                       state*Ripper+
                       state*salemonth+
                       state*Travel_Controls+
                       state*Enclosure + 
                       state*Transmission + 
                       state*Blade_Type,
                       data = train)
                     
xTest <- model.matrix(~state + saleyear + salemonth + fiSecondaryDesc + MachineAgeCat + Ripper + 
                       Travel_Controls + Enclosure + 
                       Transmission + Blade_Type + 
                       fiSecondaryDesc*MachineAgeCat + 
                       Enclosure*MachineAgeCat + 
                       Ripper*MachineAgeCat + 
                       Blade_Type*MachineAgeCat +
                       state*saleyear + 
                       state*MachineAgeCat + 
                       state*fiSecondaryDesc +
                       state*Ripper+
                       state*salemonth+
                       state*Travel_Controls+
                       state*Enclosure + 
                       state*Transmission + 
                       state*Blade_Type,
                      data = test)
                     

yTrain <- log(train$SalePrice)
yTest <- log(test$SalePrice)

Let’s look at the dimensions of the training data: We have a total of 2883 prices and we are fitting a model with as many predictor variabels as there are columns in the xTrain array - this is 602. This is a case with many predictor variables compared to number of observations and it will often be advantageous to regularize the model using the LASSO. Let’s see:

fit <- cv.glmnet(xTrain,yTrain,family="gaussian")
fitOLS <- glmnet(xTrain,yTrain,family="gaussian",lambda=0.0)

The cv.glmnet fits the LASSO model to the training data. It uses a method called cross validation to pick the optimal value of the penalty paramter $\lambda$ (see the reference above for details). To compare with the standard least squares framework, we make a second call to the function, constraining this parameter to be zero. We then predict the prices in the test data and calculate the same fit criteria as above:

yTestPredict <- predict(fit, newx = xTest, s = "lambda.min")
yTestPredictOLS <- predict(fitOLS, newx = xTest)

yTrainPredict <- predict(fit, newx = xTrain, s = "lambda.min")
yTrainPredictOLS <- predict(fitOLS, newx = xTrain)

AllResults <- bind_rows(
  data.frame(MAE = mean(abs(yTest-yTestPredict)),
             RMSE = sqrt(mean((yTest-yTestPredict)**2)),
             Sample = "Test",
             Model = "LASSO",
             stringsAsFactors = F
            ),
  data.frame(MAE = mean(abs(yTest-yTestPredictOLS)),
             RMSE = sqrt(mean((yTest-yTestPredictOLS)**2)),
             Sample = "Test",
             Model = "LS",
             stringsAsFactors = F
  ),
  data.frame(MAE = mean(abs(yTrain-yTrainPredict)),
             RMSE = sqrt(mean((yTrain-yTrainPredict)**2)),
             Sample = "Train",
             Model = "LASSO",
             stringsAsFactors = F
  ),
  data.frame(MAE = mean(abs(yTrain-yTrainPredictOLS)),
             RMSE = sqrt(mean((yTrain-yTrainPredictOLS)**2)),
             Sample = "Train",
             Model = "LS",
             stringsAsFactors = F
  )
)

AllResults %>%
  gather(Metric,Value,-Sample,-Model) %>%
  ggplot(aes(x=Model,y=Value,fill=Model)) + geom_bar(stat='identity') + facet_grid(Sample~Metric) +
  theme(legend.position = "none")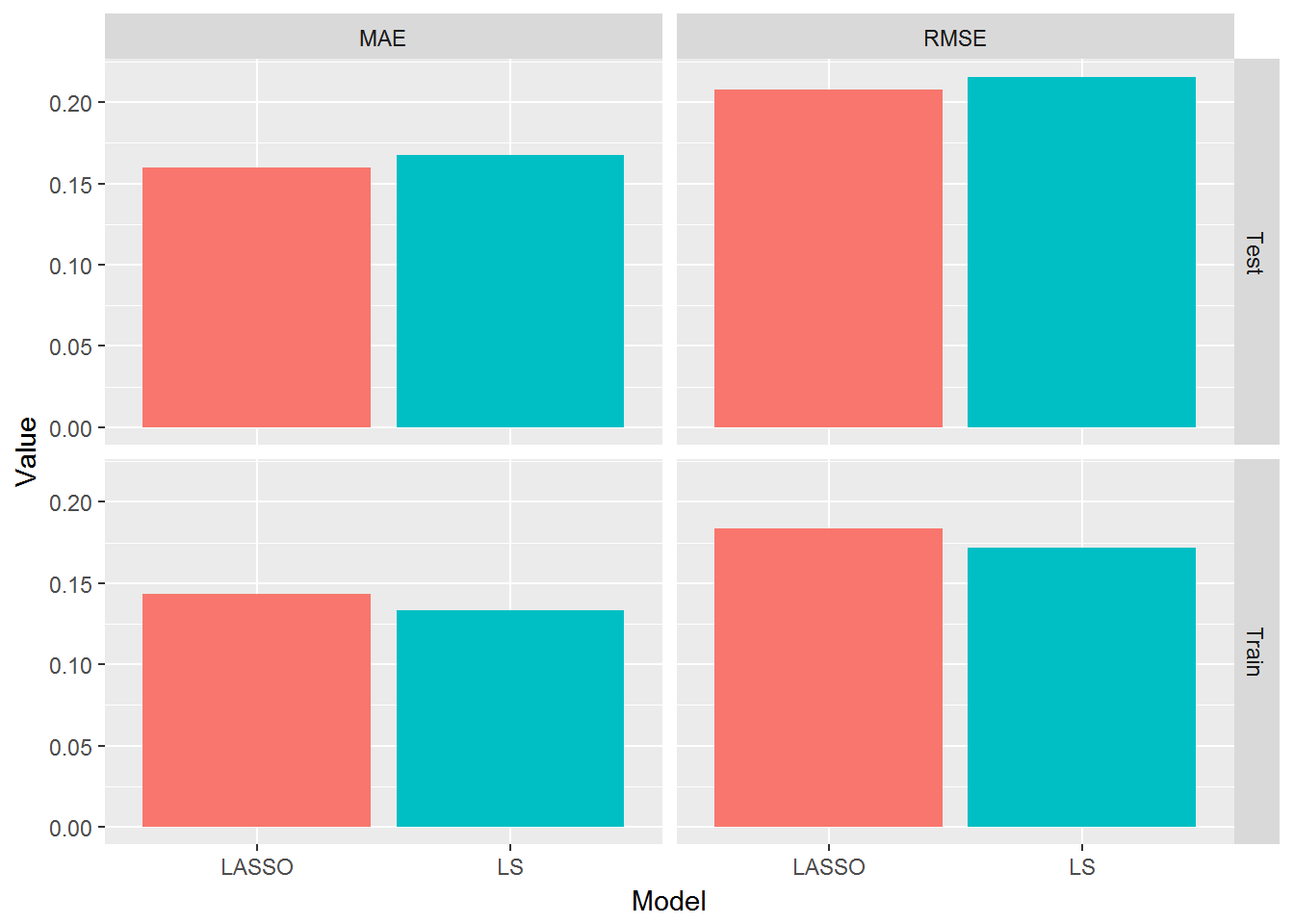

This is a nice demonstration of why you need to evaluate models on test data and not on the training data. Notice how LS does better in the training data but worse in the test data where LASSO is better.